Gráficos De Funções
Função crescente
Uma função f é crescente em um intervalo se, e somente se, à medida que os elementos do domínio crescem, suas imagens também crescem. Veja:
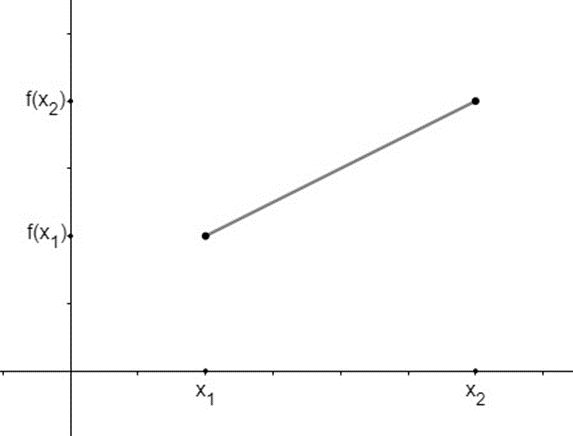
Observe que x1 > x2 e o mesmo ocorre com a imagem, assim, podemos estabelecer uma condição algébrica para que a função f seja crescente.
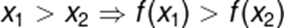
Função decrescente
Uma função f é decrescente em um intervalo se, e somente se, à medida que os elementos do domínio crescem, suas imagens decrescem. Veja:
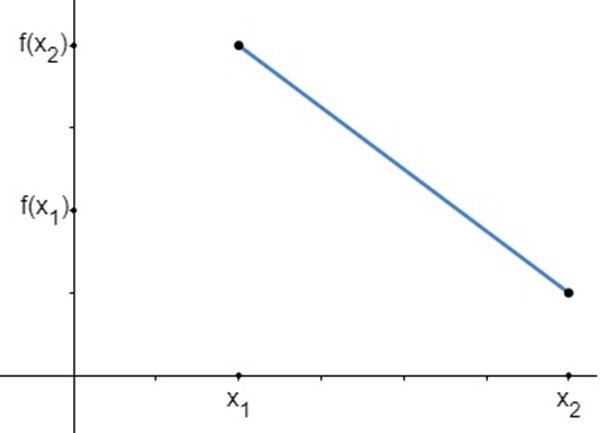
Veja que, no domínio da função, temos que x1 > x2, entretanto isso não ocorre na imagem da função, em que f(x1) < f(x2). Assim podemos estabelecer uma condição algébrica para funções decrescentes. Veja:
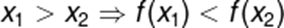
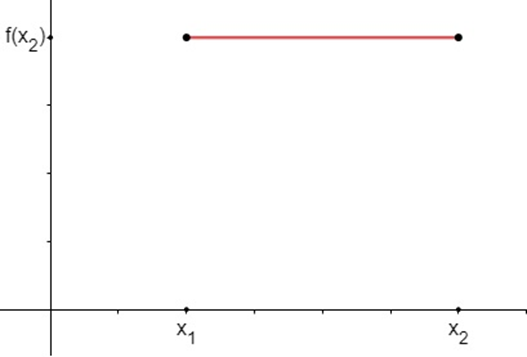
Função constante
Como o próprio nome diz, uma função é constante quando, para qualquer valor do domínio, o valor da imagem é sempre o mesmo.
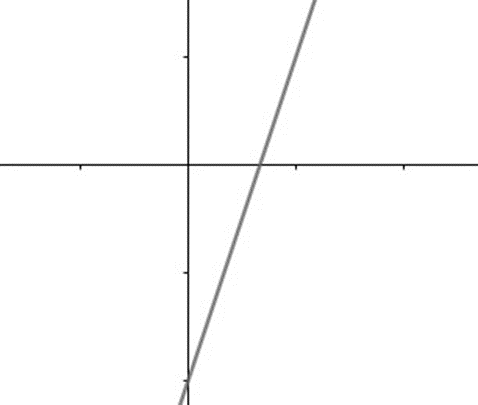
Função afim
é escrita na forma:
f(x) = ax + b
Em que a e b são números reais, a é diferente de zero, e o seu gráfico é uma reta. A função possui domínio real e contradomínio também real.
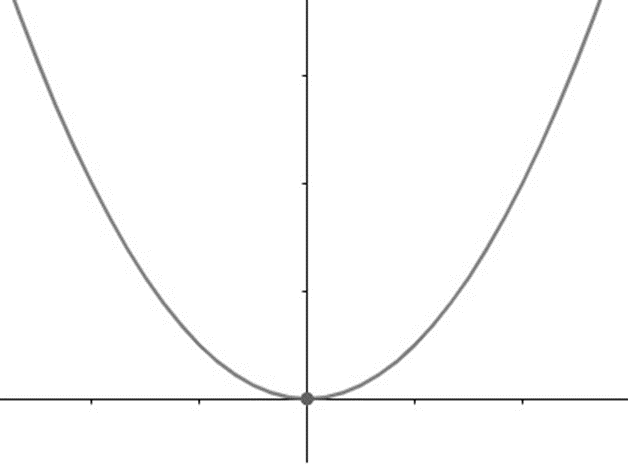
Função quadrática
é dada por um polinômio de grau dois, assim:
f(x) = ax2 + bx + c
Em que a, b e c são números reais com a diferente de zero, e seu gráfico é uma parábola. A função também possui domínio e contradomínio reais.
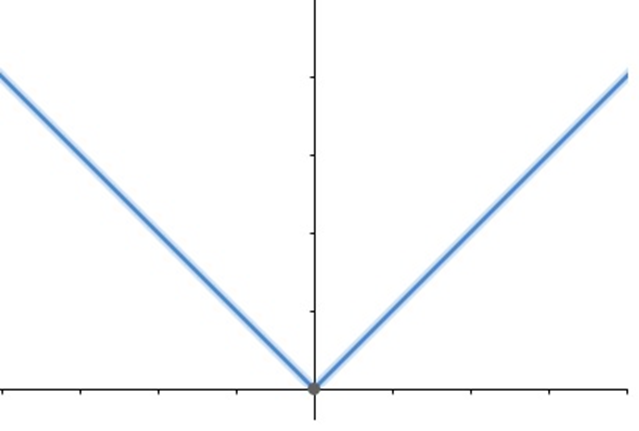
Função modular
com variável x encontra-se dentro do módulo e algebricamente é expressa por:
f(x) = |x|
A função também possui domínio e contradomínio reais, ou seja, podemos calcular o valor absoluto de qualquer número real.
Função exponencial
apresenta a variável x no expoente. Ela também possui domínio real e contradomínio real e é descrita algebricamente por:
f(x) = ax
Em que a é um número real maior que zero.
Função logarítmica
possui a variável no logaritmando e o domínio formado por números reais maiores que zero.
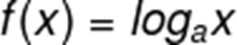

Funções trigonométricas
As funções trigonométricas possuem a variável x envolvendo as razões trigonométricas, as principais são:
f(x) = sen(x)
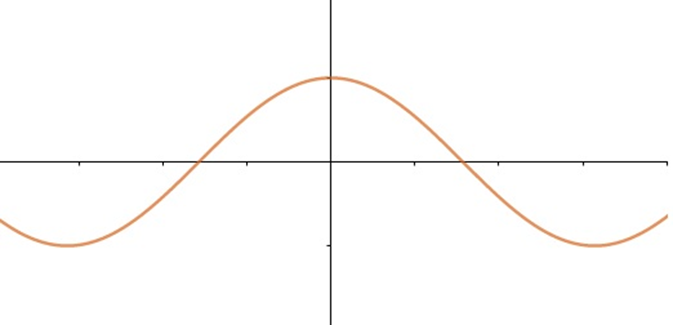
f(x) = cos(x)
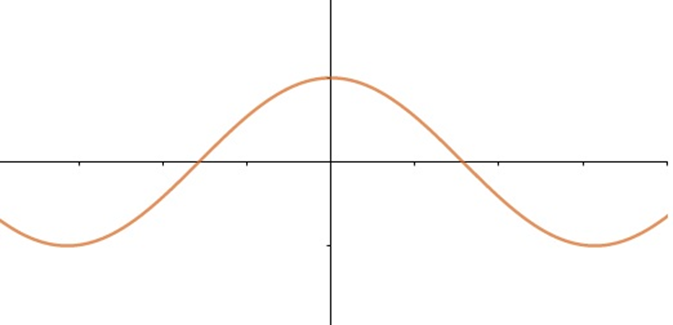
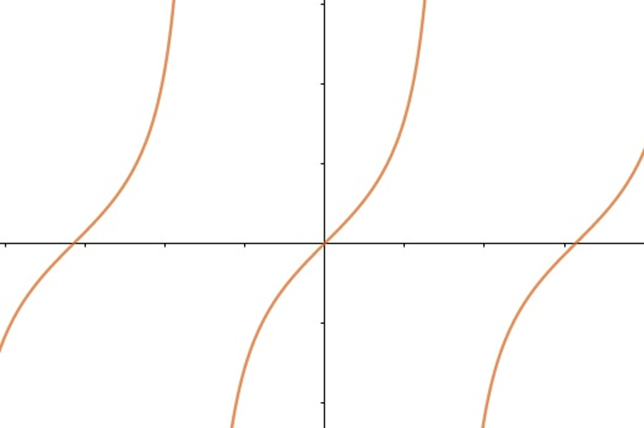
f(x) = tg(x)
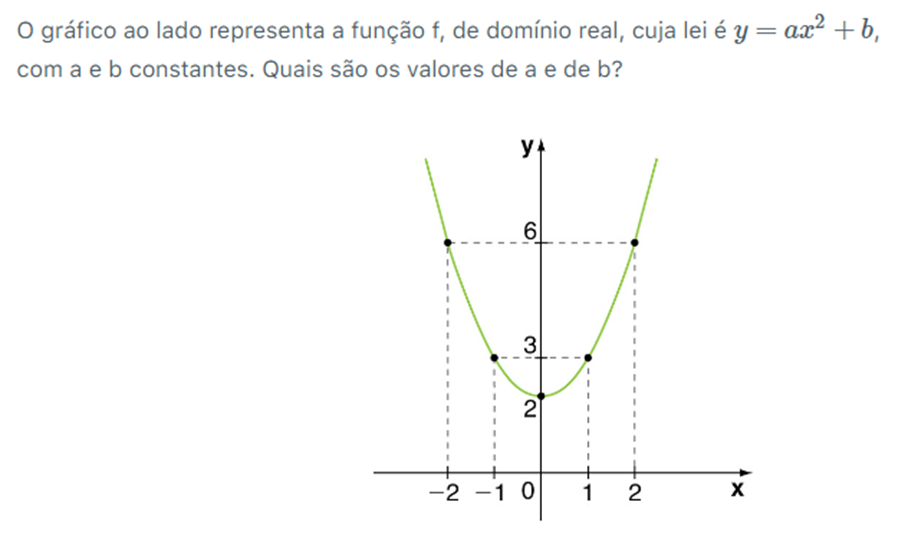
Exercícios
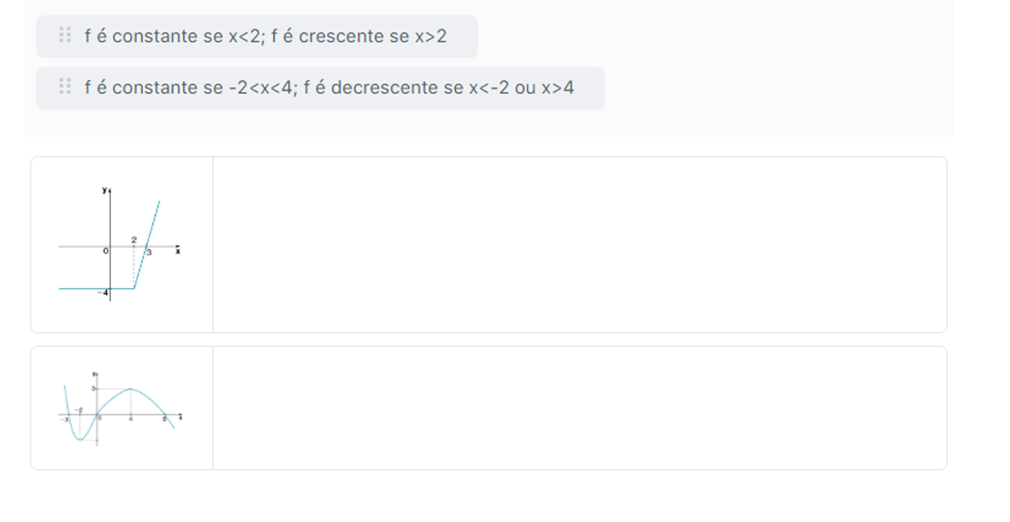
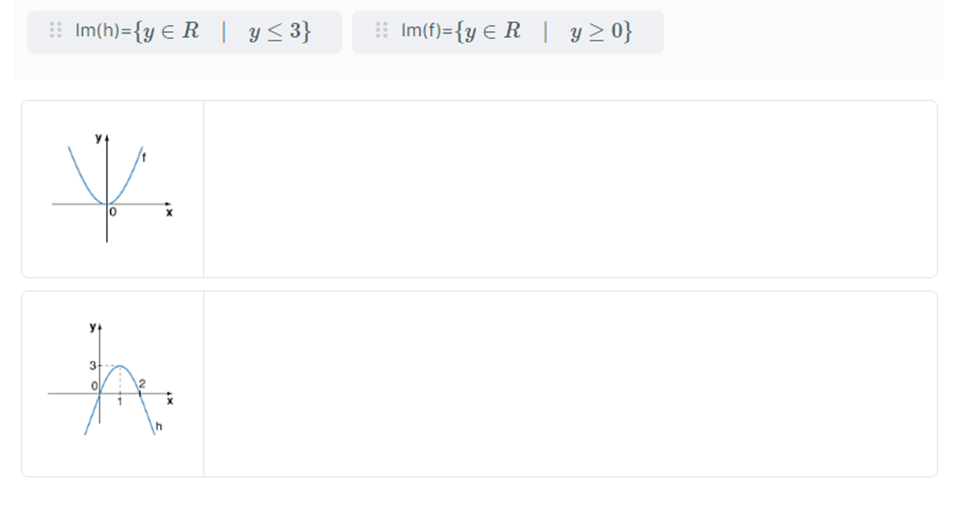


Comentários