Conjuntos de números reais

O conjunto dos números reais é representado por R. Esse conjunto é formado pelos números racionais (Q) e irracionais (I). Assim, temos que R = Q ∪ I. Além disso, N, Z, Q e I são subconjuntos de R.

Subconjuntos dos Números Reais

R*= {x ∈ R│x ≠ 0}: conjunto dos números reais não-nulos.

R+ = {x ∈ R│x ≥ 0}: conjunto dos números reais não-negativos.

R*+ = {x ∈ R│x > 0}: conjunto dos números reais positivos.

R– = {x ∈ R│x ≤ 0}: conjunto dos números reais não-positivos.

R*– = {x ∈ R│x < 0}: conjunto dos números reais negativos.

Há ainda um subconjunto relacionado com os números reais que são chamados de intervalos. Sejam a e b números reais e a < b, temos os seguintes intervalos reais:

Intervalo aberto de extremos: ]a,b[ = {x ∈ R│a < x < b}

Intervalo fechado de extremos: [a,b] = {x ∈ R│a ≤ x ≤ b}

Intervalo aberto à direta (ou fechado à esquerda) de extremos: [a,b[ = {x ∈ R│a ≤ x < b}

Intervalo aberto à esquerda (ou fechado à direita) de extremos: ]a,b] = {x ∈ R│a < x ≤ b}

Exercícios resolvido:

Durante a aula de Matemática, a professora pediu aos estudantes que eles listassem números racionais que estejam necessariamente entre os números 8 e 10. Os números escolhidos pelos estudantes foram:

Todos eles acertaram, exceto:

A) Amanda.

B) Bruna.

C) Camila.

D) Daniel.

E) Everaldo.

Resposta:

Dos números listados, todos são racionais, exceto a raiz não exata descrita por Bruna.

2 – Dividir um número por 0,125 equivale a multiplicá-lo por:

A) 1/125.
B) 1/8.
C) 8.
D) 12,5.
E) 80.

Resposta:

Vamos reescrever o número como uma fração irredutível:

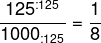
3 – Dados os números:

0; 144; – 144; 25; – 25/4; 2,45/4; – 2,45; 1; – 1; √7; –√7; √–7
                                

a) Quais desses números pertencem ao conjunto dos números naturais?

b) Quais desses números pertencem ao conjunto dos números inteiros?

c) Quais desses números pertencem ao conjunto dos números racionais?

d) Quais desses números pertencem ao conjunto dos números irracionais?

e) Quais desses números pertencem ao conjunto dos números reais?

f) Quais desses números não pertencem a nenhum dos conjuntos acima?

Respostas:

a) O conjunto dos números naturais é formado por todos os números inteiros positivos. Dessa maneira, os únicos elementos pertencentes a esse conjunto são 144 e 25.

b) O conjunto dos números inteiros é formado pelos números positivos, negativos e zero. Portanto, os representantes dos números inteiros nessa lista são: 0; 144; – 144; 25 e – 25.

c) O conjunto dos números racionais é formado por qualquer número que possa ser escrito como uma fração em que o numerador é um número inteiro e o denominador é um número natural. Dessa maneira, qualquer número que cumpra uma das três seguintes exigências é um número racional:

1 – Frações
2 – Números decimais com um número finito de casas após a vírgula
3 – Dízimas periódicas

Números que cumprem uma dessas três exigências podem ser escritos na forma de fração e, por isso, são números decimais. Tendo dito isso, é possível mostrar que qualquer número inteiro é resultado de uma divisão (por isso, pode ser escrito na forma de fração), portanto, os números inteiros também são racionais.

Na lista acima, os números racionais são:

0; 144; – 144; 25; – 25; 2,45; – 2,45; 1/4 e – 1/4
                                                        

d) Todos os números que não podem ser escritos na forma de fração são componentes do conjunto dos números irracionais. Os exemplos desses números geralmente possuem um dos dois formatos seguintes:

1 – Decimais com infinitas casas após a vírgula
2 – Raízes não exatas

Na lista acima, os números irracionais são: √7 e –√7

e) O conjunto dos números reais é formado pela união entre os conjuntos dos números racionais e irracionais. Portanto, todos os números inteiros, decimais, dízimas periódicas e raízes exatas ou inexatas são números reais.

Na lista acima, os números reais são:

0; 144; – 144; 25; – 25/4; 2,45/4; – 2,45; 1; – 1; √7; –√7
                                          

f) O único número que não é real nessa lista é √–7, pois é impossível encontrar um número real que, multiplicado por ele mesmo, tenha como resultado –7.