Questões da Prova OBMEP 2011 – Nível 3. Resolva todas as provas da OBMEP aqui.
Teste de Teoremas dos senos e cossenos Matemática 2ª série
Resumo de Exercício
0 de 31 Questões concluídos
Questões:
Em formação
Você já completou o exercício antes. Portanto, você não pode iniciá-lo novamente.
Exercício está carregando…
Você deve entrar ou se inscrever para iniciar o exercício.
Você precisa primeiro terminar os seguintes:
Resultados
Resultados
0 de 31 questões respondidas corretamente
Seu tempo:
O tempo passou
Você alcançou 0 de 0 Ponto(s), (0)
Ponto(s) ganho(s): 0 de 0, (0)
0 Redação(ões) Pendente(s) (Ponto(s) Possível(is): 0)
| Pontuação média | |
| Sua pontuação |
Categorias
- Não categorizado 0%
Você precisa melhorar! Você acertou menos que 70% das questões Tente novamente!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
Muito bom, Você acertou mais que 70% das questões, você passou!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
Parabéns! Você acertou mais que 90% das questões. Siga para os próximos exercícios!
Revise suas questões e caso esteja com dúvidas? Faça sua pergunta no Fórum
| Pos. | Nome | Data | Pontos | % |
|---|---|---|---|---|
| A tabela está carregando | ||||
| Seja o(a) primeiro a participar! | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- Atual
- Revisar
- Respondidas
- Correto
- Incorreto
- Questão 1 de 31
1. Questão
(UFPR) Um triângulo possui lados de comprimento 2 cm e 6 cm². Qual é a medida do terceiro lado desse triângulo?
CorretoIncorreto - Questão 2 de 31
2. Questão
(UPE) João está procurando cercar um terreno triangular que ele comprou no campo. Ele sabe que dois lados desse terreno medem, respectivamente, 10 m e 6 m e formam entre si um ângulo de 120°. O terrenno será cercado com três voltas de arame farpado. Se o preço do metro do arame custa R$5,00, qual o valor gasto por João com a compra do arame?
Dados: sen de 120° = \(\frac {\sqrt { 3 }}{2}
cos de 120° = – \frac {1}{2}\)CorretoIncorreto - Questão 3 de 31
3. Questão
(UFRGS-RS) Os lados de um losango medem 4 e um dos seus ângulos 30°. A medida da diagonal menor do losango é:
CorretoIncorreto - Questão 4 de 31
4. Questão
(PUC-RJ) Seja um hexágono regular ABCDEF. A razão entre os comprimentos dos segmentos \(\bar { AC } e \bar { AB } \)é igual a:
CorretoIncorreto - Questão 5 de 31
5. Questão
(EEAR-SP) Seja um triângulo inscrito em uma circunferência de raio R. Se esse triângulo tem um ângulo medindo 30°, seu lado oposto a esse ângulo mede
CorretoIncorreto - Questão 6 de 31
6. Questão
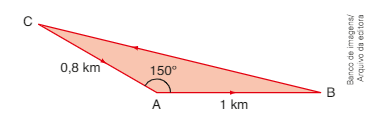
(UFSM-RS) A caminhada é uma das atividades físicas que, quando realizada com frequência, torna-se eficaz na prevenção de doenças crônicas e na melhora da qualidade de vida.
Para a prática de uma caminhada, uma pessoa sai do ponto A, passa pelos pontos B e C e retorna ao ponto A, conforme trajeto indicado na figura.Dado: \(\sqrt { 2 }\) = 1,7

Quantos quilômetros ela terá caminhado, se percorrer todo o trajeto?
CorretoIncorreto - Questão 7 de 31
7. Questão
(UFJF-MG) Uma praça circular de raio R foi construída a partir da planta a seguir:

/os segmentos \(\bar { AB }, \bar { BC } e \bar { CA }\) simbolizam ciclovias construídas no interior da praça, sendo que AB = 80 m. De acordo com a planta e as informações dadas, é correto afirmar que a medida de R é igual a:
CorretoIncorreto - Questão 8 de 31
8. Questão
(UEL-PR) Uma cidade planejada foi construída com seu sistema de esgoto obedecendo à esquematização de uma malha linear representada no gráfico ao lado, onde cada vértice dista do outro de uma unidade.
Os pontos A e B representam duas casas e o ponto O representa a origem de uma confluência de canos que necessitam de uma “luva de união”. O valor do seno do ângulo \(\theta\) que a luva de união em O possui é: CorretoIncorreto
CorretoIncorreto - Questão 9 de 31
9. Questão
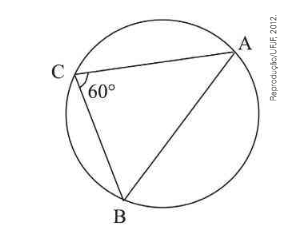
(PUC-SP) Leia com atenção o problema proposto a Calvin na tira seguinte.

Supondo que os pontos A, B e C sejam vértices de um triângulo cujo ângulo do vértice A mede 60°, então a resposta correta que Calvin deveria encontrar para o problema é, em centímetros:
CorretoIncorreto - Questão 10 de 31
10. Questão
(UFRGS-RS) No triângulo representado na figura ao lado, AB e AC têm a mesma medida, e a altura relativa ao lado BC é igual a \(\func {2}{3}\) da medida de BC. Com base nesses dados, o cosseno do ângulo CAB é:
 CorretoIncorreto
CorretoIncorreto - Questão 11 de 31
11. Questão
(Mack-SP) Num retângulo de lados 1 cm e 3 cm, o seno do menor ângulo formado pelas diagonais é:
CorretoIncorreto - Questão 12 de 31
12. Questão
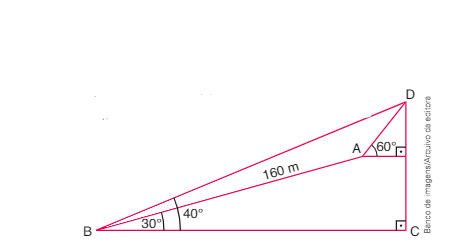
(Cefet-MG) Um grupo de escoteiros pretende escalar uma montanha até o topo, representado na figura ao lado pelo ponto D, visto sob ângulos de 40° do acampamento B e de 60° do acampamento A.
Dado: seno 20° = 0,342
Considerando que o percurso de 160 m entre A e B é realizado segundo um ângulo de 30° em relação à base da montanha, então, a distância entre B e D, em metros, é de, aproximadamente CorretoIncorreto
CorretoIncorreto - Questão 13 de 31
13. Questão
(Insper-SP) Partindo de um ponto A, um avião deslocava-se, em linha reta, com velocidade v km/h. Após duas horas, quando se encontrava no ponto B, o avião desviou \(\alpha\) graus de sua rota original, conforme indica a figura, devido às condições climáticas. Mantendo uma trajetória reta, o avião voou mais uma hora com a mesma velocidade v km/h atgé atingir o ponto C
Dados: sen \(\alpha = \frac {\sqrt { 7 }}{4}
cos \alpha = \frac {3}{4} \)
A distância entre os pontos A e C, em quilômetros, é igual a
CorretoIncorreto - Questão 14 de 31
14. Questão
(UFRGS-RS) As medidas dos lados de um triângulo são proporcionais a 2,2 e 1. Os cossenos de seus ângulos internos são, portanto
CorretoIncorreto - Questão 15 de 31
15. Questão
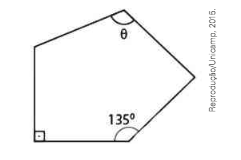
(Unicamp-SP) A figura a seguir exibe um pentágono com todos os lados de mesmo comprimento.

A medida do ângulo \(\)\theta\(\) é igual a
CorretoIncorreto - Questão 16 de 31
16. Questão
(Ufes) Duas viaturas policiais A e B perseguem um carro suspeito C numa grande cidade. A viatura A possui um radar que informa ao comando central que a distância dela até B é de 8 km e a distância dela até C é 6 km. A viatura B possui um aparelho que informa ao comando que, nesse instante, o ângulo \(A\hat { B }C\) é de 45°. Sabendo que o carro C está mais próximo de A do que de B, calcule a distância em km, entre B e C. A resposta é
CorretoIncorreto - Questão 17 de 31
17. Questão
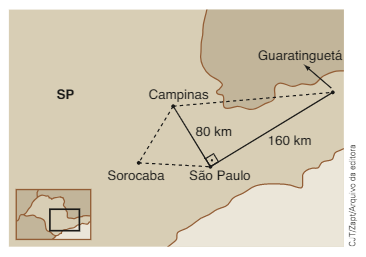
(Vunesp) Um professor de geografia forneceu a seus alunos um mapa do estado de São Paulo, que informava que as distâncias aproximadas em linha reta entre os pontos que representam as cidades de São Paulo e Campinas e entre os pontos que representam as cidades de São Paulo e Guaratinguetá eram, respectivamente, 80 km e 160 km. Um dos alunos observou, então, que as distâncias em linha reta entre os pontos que representam as cidades de São Paulo, Campinas e Sorocaba formavam um triiângulo equilátero. Já um outro aluno notou que as distâncias em linha reta entre os pontos que representam as cidades de São Paulo, Guaratinguetá e Campinas formavam um triângulo retângulo, conforme mostra o mapa.

Com essas informações, os alunos determinaram que a distância em linha reta entre os pontos que representam as cidades de Guaratinguetá e Sorocaba, em km, é próxima de
CorretoIncorreto - Questão 18 de 31
18. Questão
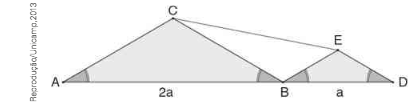
(Unicamp-SP) Na figuura abaixo, ABC e BDE são triângulos isósceles semelhantes de bases 2a e a, respectivamente, e o ângulo C\hat { A }B = 30°. Portanto, o comprimento do segmento \bar { CE } é:
 CorretoIncorreto
CorretoIncorreto - Questão 19 de 31
19. Questão
(UFPB) Ppara explorar o potencial turístico de uma cidade, conhecida por suas belas paisagens montanhosas, o governo pretende construir um teleférico, ligando o terminal de transportes coletivos ao pico de um morro, conforme a figura a seguir.

Para a construção do teleférico, há duas possibilidades:
- o ponto de partida ficar localizado no terminal de transportes coletivos (ponto A), com uma parada intermediária (ponto B) e o ponto de chegada localizado no pico do morro (ponto C);
- o ponto de partida ficar localizado no ponto A e o de chegada localizado no ponto C, sem parada intermediária.
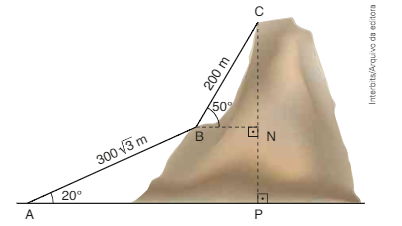
Supondo que \(\)\bar { AB } = 300 \sqrt { 3 } m, \bar { BC } = 200 m, B\hat { A }P = 20° e C\hat { B }N = 50°, é correto afirmar que a distância entre os pontos A e C é de:
CorretoIncorreto - Questão 20 de 31
20. Questão
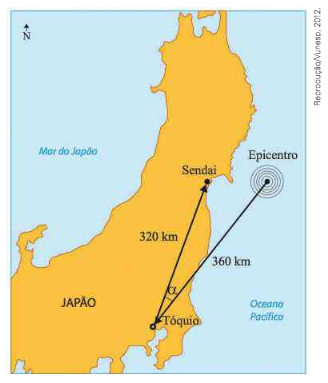
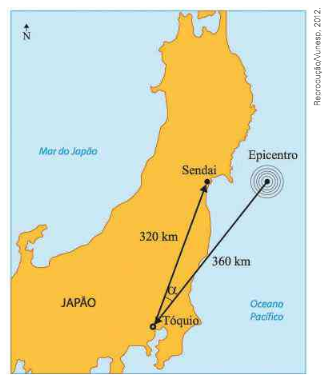
(Vunesp) No dia 11 demarço de 2011, o Japão foi sacudido por terremoto com intensidade de 8,9 na Escala Richter, com o epicentro no Oceano Pacífico, a 360 km de Tóqui, seguido de tsunami. A cidade de Sendai, a 320 km a nordeste de Tóquio, foi atingida pela primeira onda do tsunami após 13 minutos. (O Estado de S. Paulo, 13.3.2011. Adaptado)



Baseando-se nos dados fornecidos e sabendo que \( cos \alpha = 0,934, onde \alpha é o ângulo Epicentro-Tóquio-Sendai, é que { 2 }^{ 8 } . { 3 }^{ 2 } . 93,4 \simeq 215100, a velocidade média, em km/h, com que a 1ª onda do tsunami atingiu a cidade de Sendai foi de:\)
CorretoIncorreto - Questão 21 de 31
21. Questão
(Fuvest-SP) No losanago ABCD de lado 1, representado na figura, tem-se que M é o ponto médio de \(\bar { AB }, N é o ponto médio de \bar { BC } e MN = \frac {\sqrt { 14 }}{4}. Então DM é igual a:\)
CorretoIncorreto - Questão 22 de 31
22. Questão
(Mack-SP) Três ilhas, A, B e C, aparecem num mapa em escala 1:10000, como na figura abaixo:

Das alternativas, a que melhor aproxima a distância entre as ilhas A e B é:
CorretoIncorreto - Questão 23 de 31
23. Questão
(Fatec-SP) Sejam \(\alpha, \beta e \gamma as medidas dos ângulos internos de um triângulo.
Se \func {sen \alpha}{sen \beta} = \func {3}{5}, \func {sen \alpha}{sen \gamma} = 1 e o perímetro do triângulo é 44, então a medida do maior lado desse triângulo é:\)CorretoIncorreto - Questão 24 de 31
24. Questão
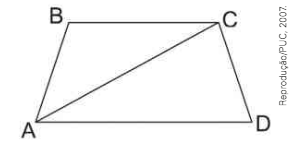
(PUC-MG) Quatro estações de um metrô ocupam os vértices de um trapézio isósceles, conforme indicado na figura. A linha \(\)\bar { AD } mede 15 km, a linha \bar { AB } tem 8 km e o ângulo entre as linhas \bar { BC } e \bar { CD }, o maior do trapézio, mede 120°. Com base nessas informações, é correto afirmar que a extensão da linha \bar { AC }, em quilômetros, é igual a:
 CorretoIncorreto
CorretoIncorreto - Questão 25 de 31
25. Questão
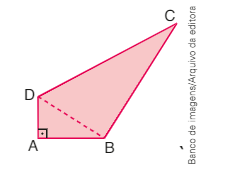
(UFSE) \(No quadrilátero ABCD da figura a seguir, tem-se que:
- ângulo B\hat { A } D é reto;
- BD = 3 cm e CD = 6 cm;
- B\hat { D } C = 60°;
- a tangente de A\hat { D } B é o dobro da tangente de A\hat { B } D [latex]

a)[latex] AB = \sqrt { 6 } cm
b) O seno de um dos ângulos agudos no triângulo ABD é igual a \frac {\sqrt { 3 }}{3}
c) BC = 3\sqrt { 3 } cm
d) O perímetro do quadrilátero ABCD é igual a (6\sqrt { 6 } + 4\sqrt { 3 }) cm
e) AC = \sqrt { 33 + \sqrt { 6 } } cm\)CorretoIncorreto - Questão 26 de 31
26. Questão
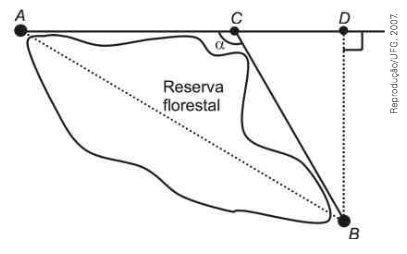
(UFG-GO) Uma empresa de engenharia deseja construir uma estrada ligando os pontos A e B, que estão situados em lados opostos de uma reserva florestal, como mostra a figura abaixo.

A empresa optou por construir dois trechos retilíneos, detonados pelos segmentos AC e CB, ambos com o mesmo comprimento. Considerando que a distância de A até B, em linha reta, é igual ao dobro da distância de B e D, o ângulo \(\alpha\), formado pelos dois trechos retilíneos da estrada, mede:
CorretoIncorreto - Questão 27 de 31
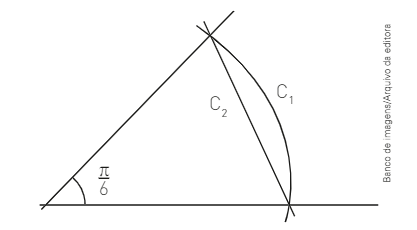
27. Questão
(Fuvest-SP) Numa circunferência, \({ C }_{ 1 } é o comprimento de arco de \func{\pi}{6} radianos e { C }_{ 2 } é o comprimento da secante determinada por esse arco, como ilustrado na figura a seguir. Então, a razão \func {{ C }_{ 1 }}{{ C }_{ 2 }} é igual a \func{\pi}{6} multiplicado por:\)
 CorretoIncorreto
CorretoIncorreto - Questão 28 de 31
28. Questão
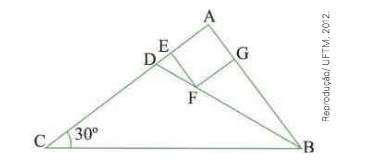
(UFTM-MG) Na figura, AEFG é um quadrado, e \(\bar { BD } divide o ângulo A\hat { B } C ao meio.

Sendo CD = 2\sqrt { 3 } cm, o lado do quadrado AEFG, em centímetros, mede:\)
CorretoIncorreto - Questão 29 de 31
29. Questão
(ITA-SP) \(Considere o triângulo ABC de lados a = \bar {BC}, b = \bar {AC} e c = \bar {AB} e ângulos internos \alpha = C\hat{A}B, \beta A\hat{B}C e \gamma = B\hat{C}A. Sabendo-se que a equação { x }^{ 2 } – 2bx cos\alpha + { b }^{ 2 } – { a }^{ 2 } = 0 admite c como raiz dupla, pode-se afirmar que:\)
CorretoIncorreto - Questão 30 de 31
30. Questão
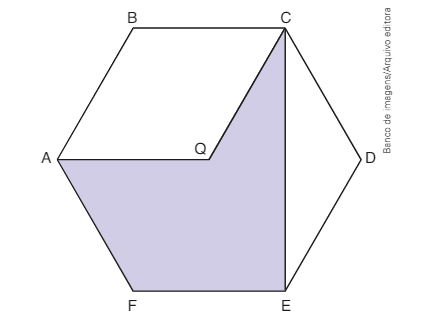
(FGV-SP) Na figura, ABCDEF é um hexágono regular de lado 1 dm, e Q é o centro da circunferência inscrita a ele.

O perímetro do polígono AQCEF, em dm, é igual a
CorretoIncorreto - Questão 31 de 31
31. Questão
(Uece) No triângulo MPQ, seja PH a altura relativa ao vértice P. O ponto H, no lado MQ, divide-o em dois segmentos cujas medidas são respectivamente 3 cm e 2 cm. Se a medida da altura (segmento PH) é 6 cm, então, a medida do ângulo interno do vértice P é igual a
CorretoIncorreto