Sequência de Fibonacci
Sequência de Fibonacci é uma sucessão de números que obedecem um padrão em que cada elemento subsequente é a soma dos dois anteriores.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584…
A sequência de Fibonacci é definida pela seguinte fórmula:
[latex]{ F }_{ n }={ F }_{ n-1 }+{ F }_{ n-2 }[/latex]
Assim, temos:
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
e assim sucessivamente.
Mas agora, reflita sobre o seguinte:
O que há em comum entre pinturas do período renascentista, obras arquitetônicas da Antiguidade Clássica, a estrutura espiral de conchas de alguns seres vivos marinhos e o crescimento populacional?
Sim! Ela mesmo!
A sequência de Fibonacci se originou em um estudo sobre cálculo da multiplicação de coelhos e foi apresentada em seu primeiro livro, Liber abaci, como solução para o crescimento populacional de coelhos
O objetivo era responder a seguinte pergunta:

Quantos pares de coelhos existirão daqui a um ano?
( E ai, sabe como resolver isso? Deixe seu comentário)
A sequência de Fibonacci corresponde às medidas dos lados dos quadrados que montam a espiral logarítmica muito encontrada em formas da natureza como a do molusco náutico ( Nautilus pompilius) e na distribuição de pétalas de diversas flores. Foi identificada pelo matemático italiano Leonardo de Pisa (1170-1250) em seu livro Liber Abaci, de 1202, quando calculou o crescimento das populações de coelhos a partir de um casal.

Leonardo de Pisa que por ser filho de Guglielmo dei Bonacci também era chamado de Leonardo Fibonacci (filho de Bonacci), viajou para o Egito, Síria e Grécia por conta dos negócios de seu pai. Teve um professor muçulmano que lhe transmitiu os conhecimentos matemáticos dos árabes e dos hindus. O Liber Abaci ( Livro do Ábaco) também teve grande importância na divulgação, na Europa, do sistema de numeração criado pelos hindus.
Liber Abaci foi um dos primeiros livros ocidentais a descrever os algarismos arábicos, introduzindo na Europa a numeração árabe ( em substituição a numeração romana) e esclarecendo o funcionamento desta numeração e do zero.
O Número de Ouro φ
Em 1753, o escocês Robert Simson descobriu que dividindo-se esses números pelos seus antecessores ( que vêm antes) obtém-se uma sequência de frações cuja a razão se aproxima de φ (Phi).
[latex]\frac { 1 }{ 1 } ,\frac { 2 }{ 1 } ,\frac { 3 }{ 2 } ,\frac { 5 }{ 3 } ,\frac { 8 }{ 5 } ,\frac { 13 }{ 8 } ,\frac { 21 }{ 13 } …[/latex]
Que ficou conhecida como razão áurea φ = 1,61803398874989…
O número de ouro ou proporção áurea é uma razão representada pelo número Φ (Phi) e é um número irracional.
Acredita-se que Deus deixou sua marca no mundo através da matemática, ou seja, usou ela para construir a simetria existente em tudo. Essa simetria é representada pelo o número de ouro e simboliza o referencial de beleza.

Por representar a divina proporção, é muito utilizado no design, na arte, na arquitetura, no tamanho dos cartões de créditos, das caixas de cigarro e dos outdoors.
Curiosamente, o número de ouro está inserido em tudo que podemos imaginar: seres humanos, músicas, natureza, arquitetura, etc.
Todas as fórmulas de Fibonacci podem ser encontradas aqui.
Aplicações da Sequência de Fibonacci
Análise de mercados financeiros
O uso da sequência de Fibonacci no mercado de ações foi desenvolvido por Ralph Nelson Elliott (1871-1948), um analista financeiro norte-americano que estudou o comportamento do índice Dow Jones, da Bolsa de Valores de Nova Iorque. Elliot concluiu que existem relações entre picos e vales do gráfico da flutuação de bolsa e estas tendem a seguir razões numéricas aproximadas das razões de dois números consecutivos da sequência de Fibonacci.
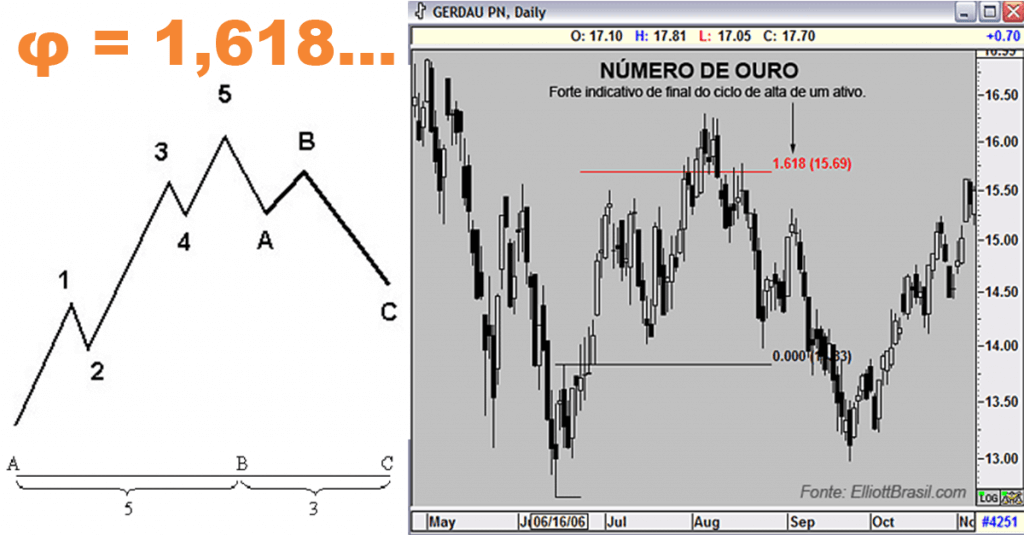
E assim, é possível calcular e prever pontos de inflexão no mercado de commodities, analisar ciclos econômicos e identificar momentos lucrativos na taxa de juros.
Triângulo de Pascal
O triângulo de Pascal e o triângulo de Pitágoras também se relacionam com a sequência de Fibonacci.
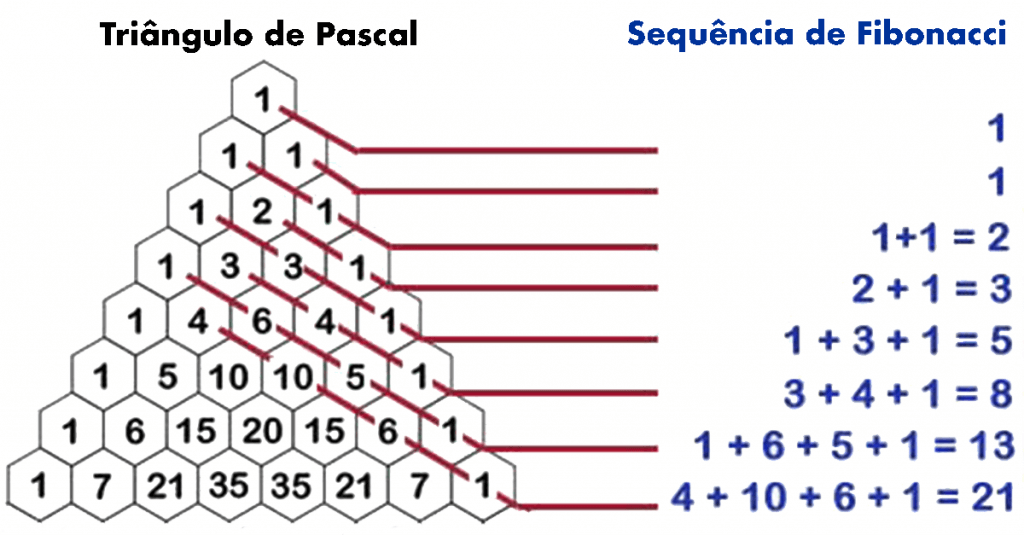
Pintura e Arte

Anatomia e o Homem Vitruviano
Leonardo Da Vinci acreditava na perfeição da figura humana e considerava as medidas e o funcionamento do corpo humano como uma analogia das medidas e funcionamento do universo, todas conectadas pela proporção do número de ouro.

Arquitetura

Ramos de troncos em árvores
Uma planta em particular, mostra os números da sequência de Fibonacci nos seus “pontos de crescimento”. Quando a planta nasce leva dois meses para crescer até que as ramificações fiquem suficientemente fortes. Sabendo que após este período a planta se ramifica todos os meses, obtemos a seguinte figura:

Uma planta que cresce de forma semelhante a esta, é a espirradeira (oleandro, louro rosa) ou cevadilha.
Desafio
Na tabela abaixo, cada número é sempre a soma dos dois que vêm antes dele. Alguns números já estão no lugar, qual é o número da última casa?

Veja também: Toda Matemática Básica
Exercício
Vamos praticar? Resolva o exercício online sobre Sequência de Fibonacci. Ao final você recebe sua nota.
Exercício Sequência de Fibonacci
Veja também: Todos Exercícios de Matemática
Dica
Donald no País da Matemágica e O Número de Ouro – Assista um ótimo filme que aborda a Sequência de Fibonacci.
Inscreva-se: Canal Matemática Zup

Cadê o vídeo completo que você disse que ia estar aqui, sobre a sequência de Fibonacci e o problema dos coelhos?
Resultado da sequência é= 92736
o resultado é 75025
17711 + X = 46368
X = 46368 – 17711
X = 28657
Resultado = 46368 + 28657
Resultado = 75025
Tambem poderia ser:
46.368 x 1,618034 = 75025
46368×1,618034=75025
Resultado = 75025
75025
75025
O resultado é 75.025
Na verdade o resultado é 75.024,99.
Basta multiplicar o último número pelo número de ouro.
Porém, pelo arredondamento e padrão Fibonacci, o número é ímpar 75.025.
Após 12 meses haverão 144 casais de coelhos, considerando que nenhum morra e que cada par ao nascer seja constituído por uma fêmea e um macho.
Neste desafio o resultado será a soma de dois numeros anteriores, assim sendo a sequência será: 1+1=2+1=3+2=5+3=8+5=13+8=21+13=34+21=55+34=89+55=144+89=233+144=377+233=610+377=987+610=1597+987=3584+1597=4181+3584=6765+4181=10946+6765=17711+10946=28657+17711=46368+28657=75025
Então o resultado será 75025.
Em resposta à questão dos coelhos eu discordo da resposta da Beatriz.
Na verdade, teremos 304 (trezentos e quatro) casais; visto que:
1 mês – 1
2 mês – 2
3 mês – 3
4 mês – 5
5 mês – 8
6 mês – 13
7 mês – 21
8 mês – 34
9 mês – 55
10 mês – 89
11 mês – 144
1 ano – 233
Somando-se a quantidade total de crias obtidas, resultara em 608 (seiscentos e oito) filhotes.
Dividindo-se por 2 temos como resultado, 304 casais.